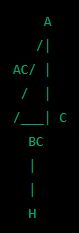16 Просмотров

Задание:

В треугольнике АВС , угол С=90°, СН и АВ, АС=15см, СН=12см, АВ=25см. Найдите проекцию катетов СВ на гипотенузу АВ. С чертежом

Ответ на задание:

Для решения задачи используем теорему Пифагора в прямоугольном треугольнике (ABC), где (​\( \angle C = 90^\circ \)​).

Теорема Пифагора:

\[ AB^2 = AC^2 + BC^2 \]

Заменяем известные значения:

\[ 25^2 = 15^2 + BC^2 \]

Решаем уравнение:

\[ BC^2 = 625 – 225 \]

\[ BC^2 = 400 \]

\[ BC = \sqrt{400} = 20 \]

Теперь у нас есть значение катета (BC), и мы можем найти проекцию катетов (CB) и (CA) на гипотенузу (AB).

Проекция катета (CB) на гипотенузу (AB) равна:

\[ CB_{\text{пр}} = \frac{BC \cdot AB}{AC} \]

Подставляем значения:

\[ CB_{\text{пр}} = \frac{20 \cdot 25}{15} = \frac{500}{15} = \frac{100}{3} \approx 33.33 , \text{см} \]

Таким образом, проекция катетов (CB) на гипотенузу (AB) составляет примерно (33.33) см.