21 Просмотров

Задание:

Три концентрические сферические поверхности радиусом r1 = 10 см, r2 = 20 см и r3 = 30 см несут заряд q = 10–8 Кл каждая. Построить графики зависимости напряженности поля от расстояния от центра сфер.

Ответ на задание:

Для определения напряженности электрического поля ( E ) от точечного заряда ( q ) на расстоянии ( r ) можно использовать закон Кулона:

\[ E = \frac{k \cdot |q|}{r^2} \]

где ( k ) – постоянная Кулона (​\( k \approx 8.99 \times 10^9 , \text{Н} \cdot \text{м}^2/\text{Кл}^2 \)​).

Для трех сферических поверхностей с зарядами ( ​\( q = 10^{-8} , \text{Кл} \)​ ) на радиусах ( ​\( r_1 = 10 , \text{см} \)​ ), (​\( r_2 = 20 , \text{см} \)​ ) и ( ​\( r_3 = 30 , \text{см} \)​ ), напряженность электрического поля будет зависеть от расстояния ( r ) до центра каждой сферы.

Давайте построим графики зависимости напряженности поля от расстояния ( r ) для каждой из сфер.

Первая сфера (радиус ( ​\( r_1 = 10 , \text{см} \)​):

\[ E_1 = \frac{k \cdot |q|}{r_1^2} \]

Вторая сфера (радиус ( ​\( r_2 = 20 , \text{см} \)​ )):

\[ E_2 = \frac{k \cdot |q|}{r_2^2} \]

Третья сфера (радиус ( ​\( r_3 = 30 , \text{см} \)​ )):

\[ E_3 = \frac{k \cdot |q|}{r_3^2} \]

Построим графики этих зависимостей.

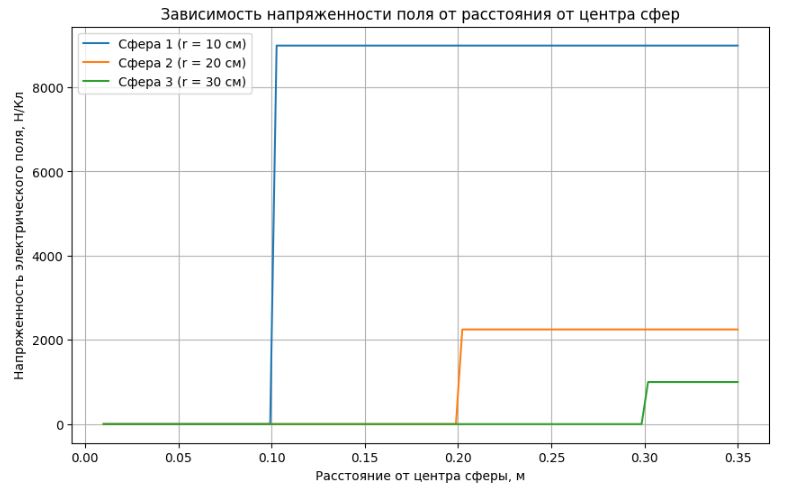
График зависимости напряженности электрического поля от расстояния до центра каждой из сфер с радиусами 10 см, 20 см и 30 см.