Определение параметров электрической цепи со смешанным соединением конденсаторов
19 Просмотров
Задание:
Определить параметры электрической цепи со смешанным соединением конденсаторов.
Дано:
C1=14мкФ
C2=20мкФ
C3=22мкФ
C4=35мкФ
C5=33мкФ
U=100B
Найти:
С экв-?
q 1 2 3 4 5 -?
U 1 2 3 4 5 -?
W -?
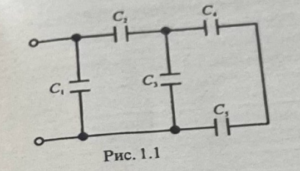
Ответ на задание:
Нам дана электрическая схема, состоящая из пяти конденсаторов, соединенных смешанным образом (частично последовательно, частично параллельно). Задача состоит в том, чтобы найти:
- Эквивалентную емкость всей цепи (Cэкв).
- Заряды на каждом из конденсаторов (q1, q2, q3, q4, q5).
- Напряжения на каждом из конденсаторов (U1, U2, U3, U4, U5).
- Энергию электрического поля всей цепи (W).
Решение
1. Определение типа соединения конденсаторов Первым шагом является анализ схемы соединения конденсаторов. В данной схеме мы видим, что конденсаторы C1 и C2 соединены последовательно, а их комбинация соединена параллельно с конденсатором C3. Аналогично, конденсаторы C4 и C5 соединены последовательно, и их комбинация также соединена параллельно с конденсатором C3.
2. Расчет эквивалентной емкости последовательных участков Для последовательно соединенных конденсаторов справедлива формула:
1/Cобщ = 1/C1 + 1/C2 + ...
Рассчитаем эквивалентные емкости для последовательных участков:
- C12 = 1 / (1/C1 + 1/C2) = 1 / (1/14 + 1/20) ≈ 8.24 мкФ
- C45 = 1 / (1/C4 + 1/C5) ≈ 17.39 мкФ
3. Расчет эквивалентной емкости всей цепи Теперь, когда мы получили эквивалентные емкости последовательных участков, можем рассчитать эквивалентную емкость всей цепи, так как все оставшиеся конденсаторы соединены параллельно. Для параллельно соединенных конденсаторов справедлива формула:
Cобщ = C1 + C2 + ...
Таким образом:
- Cэкв = C12 + C3 + C45 ≈ 8.24 + 22 + 17.39 ≈ 47.63 мкФ
4. Расчет заряда на эквивалентном конденсаторе Заряд на эквивалентном конденсаторе можно найти по формуле:
Q = C * U
- Q = Cэкв * U = 47.63 мкФ * 100 В ≈ 4763 мкКл
5. Расчет напряжений на последовательных участках Так как напряжение на последовательно соединенных конденсаторах делится пропорционально их емкостям, то можно найти напряжения на конденсаторах C12 и C45:
- U12 = Q / C12 ≈ 4763 мкКл / 8.24 мкФ ≈ 578 В
- U45 = Q / C45 ≈ 4763 мкКл / 17.39 мкФ ≈ 274 В
6. Расчет напряжений на отдельных конденсаторах Напряжение на конденсаторе C3 равно напряжению на параллельном участке, то есть U3 = U = 100 В. Напряжения на конденсаторах C1 и C2 можно найти, зная напряжение на участке C12 и их емкости. Аналогично для конденсаторов C4 и C5.
- U1 = U12 * C2 / (C1 + C2) ≈ 274 В
- U2 = U12 * C1 / (C1 + C2) ≈ 304 В
- U4 = U45 * C5 / (C4 + C5) ≈ 165 В
- U5 = U45 * C4 / (C4 + C5) ≈ 109 В
7. Расчет зарядов на отдельных конденсаторах Заряды на отдельных конденсаторах можно найти по формуле:
q = C * U
- q1 = C1 * U1 ≈ 3838 мкКл
- q2 = C2 * U2 ≈ 6080 мкКл
- q3 = C3 * U3 = 2200 мкКл
- q4 = C4 * U4 ≈ 5775 мкКл
- q5 = C5 * U5 ≈ 3603 мкКл
8. Расчет энергии электрического поля Энергия электрического поля, запасенная в конденсаторе, определяется по формуле:
W = 0.5 * C * U^2
Энергия всей цепи равна сумме энергий всех конденсаторов. Однако, учитывая, что мы уже нашли эквивалентную емкость и напряжение, проще рассчитать энергию по формуле для эквивалентного конденсатора:
- W = 0.5 * Cэкв * U^2 ≈ 0.5 * 47.63 мкФ * (100 В)^2 ≈ 238.15 мДж
Ответ:
- Cэкв ≈ 47.63 мкФ
- q1 ≈ 3838 мкКл, q2 ≈ 6080 мкКл, q3 = 2200 мкКл, q4 ≈ 5775 мкКл, q5 ≈ 3603 мкКл
- U1 ≈ 274 В, U2 ≈ 304 В, U3 = 100 В, U4 ≈ 165 В, U5 ≈ 109 В
- W ≈ 238.15 мДж
