37 Просмотров

В переводе с латинского языка тригонометрия означает «измерение треугольников». В современной интерпретации под этим определением следует понимать решение треугольников, то есть выведение всех его сторон, углов и прочих элементов на основании известных исходных данных. Принципы и положения тригонометрии широко используются в астрономии, строительстве, при межевании участков и в других областях человеческой деятельности.

Прежде чем перейти к рассмотрению тригонометрических формул, следует рассказать о, что такое тригонометрические функции. К ним относятся синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x). Последние две функции являются вспомогательными и в наши дни используются крайне редко. Основное назначение вышеупомянутых элементарных функций – изучение основ тригонометрии и исследование периодических процессов. В подавляющем большинстве случаев тригонометрические функции определяются, как отношение сторон треугольника или его определенных отрезков в единичной окружности. В современное время возникают новые определения, в частности, выражение тригонометрических функций через решения дифференциальных уравнений или же через суммы рядов. В результате мы можем существенно расширить область применения геометрии и переносить ее положения на вещественные, а в ряде случаев и на комплексные числа.

Тригонометрические формулы, отражающие основные функции, выглядят следующим образом:

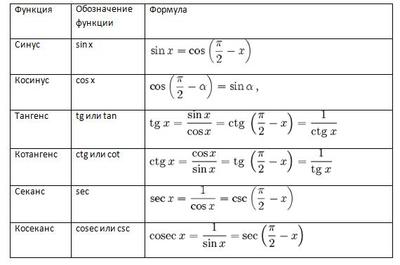
Тригонометрические формулы

В таблице указаны тригонометрические формулы, связывающие их между собой. Данные соотношения часто называют определением функций, однако это не совсем верно, поскольку определять их можно и другими способами, например, через окружность или через ряды. Отметим также, что с тригонометрическими функциями тесно связаны обратные им выражения.

Основные тригонометрические формулы, применяемые при решении задач в школах и ВУЗах, выглядят следующим образом:

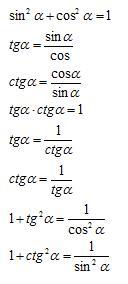
Тригонометрические формулы

Все эти тригонометрические формулы справедливы для определения общих решений треугольников, однако они могут меняться в зависимости от изменения исходных данных. Так, например, чтобы определить тригонометрические функции прямоугольного треугольника, их выражают через обозначения сторон. Для этого выделяют гипотенузу треугольника (обозначается с), прилежащий катет (обозначается b), который является стороной угла, и противолежащий катет (обозначается a), лежащий напротив угла.

Тригонометрические формулы для выражений функций через окружность или ряды также будут иметь другой вид. В первом случае на окружности берется точка, и все тригонометрические функции выражаются через отношение абсциссы и ординаты к длине отрезка от центра окружности до заданной точки. В случае с рядами математики используют свойства пределов и через основные положения теории Тейлора выводят отношения тригонометрических функций.